Math and Logic Puzzles: Redux

[StrangerCoug]

Bringing back the sudoku puzzles:

4				5	2
	5		1			3		7
		9
5					4		7
	3			1			8
	6		5					2
						7
2		1			6		9
			8	7				3

[Mitillos]

Spoiler:

4	1	3	7	5	2	8	6	9
8	5	6	1	4	9	3	2	7
7	2	9	6	8	3	1	5	4
5	8	2	3	6	4	9	7	1
9	3	4	2	1	7	6	8	5
1	6	7	5	9	8	4	3	2
3	4	8	9	2	5	7	1	6
2	7	1	4	3	6	5	9	8
6	9	5	8	7	1	2	4	3

Edit:

Spoiler: @Scigatt

I don't think your proof works. You appear to be proving some kind of converse to the statement? You end up with the assertion that the lines drawn are of equal length, but that's given by the problem statement.

[StrangerCoug]

Sudoku is good

[Scigatt]

Spoiler: @Scigatt

I don't think your proof works. You appear to be proving some kind of converse to the statement? You end up with the assertion that the lines drawn are of equal length, but that's given by the problem statement.

Spoiler:

I prove that that particular circle crosses the extended sides at the right places to recreate the original setup. Therefore, when I have the original setup, we know that circle satisfies the requirements.

[Mitillos]

Edit: Thinking about it some more.

Edit2: Yeah, I missed a couple of critical sentences there. It works.

[StrangerCoug]

Here's a more challenging sudoku I came up with that should be visually interesting as well:

6				8				4
	7		9		1		3
		8				5
	6		8		9		1
4				2				6
	2		6		7		4
		7				4
	5		3		4		2
1				7				9

[Mitillos]

Spoiler:

6	3	2	7	8	5	1	9	4
5	7	4	9	6	1	2	3	8
9	1	8	4	3	2	5	6	7
7	6	5	8	4	9	3	1	2
4	8	1	5	2	3	9	7	6
3	2	9	6	1	7	8	4	5
2	9	7	1	5	6	4	8	3
8	5	6	3	9	4	7	2	1
1	4	3	2	7	8	6	5	9

[StrangerCoug]

Correct

[StrangerCoug]

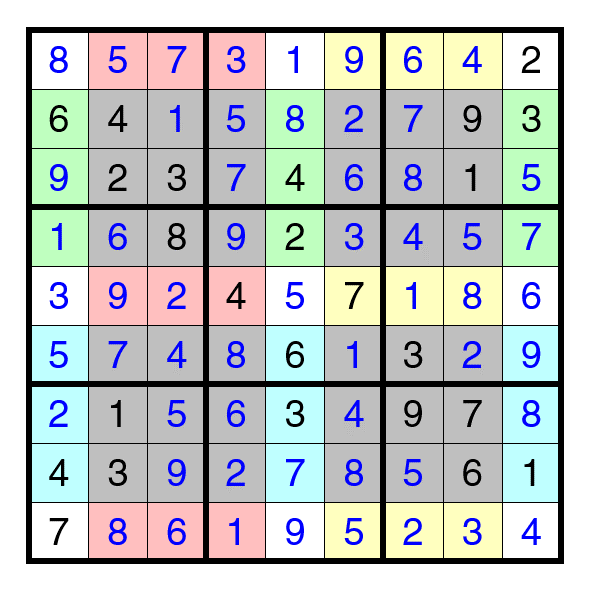
Here's another fun sudoku one, and this one is part one of a two-parter:

The below is a hyper sudoku puzzle, also known as a "windoku" puzzle. The standard rules apply except with one additional restraint: four "window panes", partly overlapping each of the nine boxes, are shaded gray, and each pane must also have the digits from 1 to 9 exactly once. Here is the puzzle:

Part 1, as in my last two questions, is to solve the windoku puzzle. Part 2 will be posted when the correct solution is posted.

[Mitillos]

Spoiler:

[StrangerCoug]

Very good Now...

Spoiler: Part two

Take the solution:

...and note that that not only do the four window panes contain every number from 1 to 9, but the cells colored pink, yellow, green, and blue in the solution grid as well as the cells left white below also contain every number from 1 to 9:


Prove that this is true in general for any hyper sudoku puzzle.

[Mitillos]

Spoiler:

Any collection of 3 rows (resp. columns) must have each number 1 to 9 exactly three times. The windows account for one copy of each number each. Since each of the green and blue (resp. pink and yellow) sets combine with two windows to make three rows (resp. columns), each of those sets must account for a copy of each number. Thus we have 8 sets (4 windows, 4 colours) each accounting for one copy of each number. The remaining (white) cells must account for the ninth and final copy of each number.

[StrangerCoug]

Looks good to me

[word321]

hmm
Ill try to keep alive this section

I guess a lot of different ppl come to this thread, so here is one constructive in nature that can (supposedly) be enjoyed by ppl with different degrees of knowledge; it also serves as basis to expand ur knowledge of math while we r at it (if u didnt know about it already)!
To solve this u will need basic algebra (think about working with the x and decomposing a number in prime factors) and know about sum and multiplication.

So first lets begin with an operation:

Module

.
We will write the module operation between 2 numbers x and y with the symbol % (x%y) and read it as "x module y".
The intuition behind module is the remainder of an integer division; 9%2=1, for example, because 9/2= 8/2+1/2; 8/2=4, but 1 is left as a remainder, as it can not be divided by 2 into an integer number.
Formally, we say that p%q=r if and only if there exists an integer n such as p=n*q+r, with r>=0 and r<q.

U can prove it if u want, but it is not necessary, that the operation is well defined and whatever formality nitpicks u have.

Modules generalize a lot of the concepts we work with, and we use that operation constantly, even if we dnt realize it. Want an example? Lets say it is 5:30 Pm; wich minute well have in 92 minutes? Those quick at calculating stuff will now it will be 7:02; it is 60+30+2 +the initial 30, rendering 60+60+2. The answer to wich minute is it is the answer to (30+92)%60; with hours, it works the same way. if it is 23:00, in 48 hours it will be 23:00, and in 5 hours it will be 4:00; that is a module by 24.

so, lets go to the challenges:


1. Prove that % is distributed over addition, that is:
(x+y)%z=(x%z+y%z)%z

Examples:
(5%3+11%3)%3=(2+2)%3=1=(5+11)%3

Hint:

Spoiler:

Lets say that x%z=p, that y%z=q; furthermore, lets say that x=m*z+p and that y=n*z+q; sum those values and reach the conclusion.

2. Prove that the sum of 2 numbers is even if and only if both numers are even or both numbers are odd

Hint:

Spoiler:

Prove that x is even if x%2=0 and odd if x%2=1, and use the above.

3. Prove that the same thing above occurs with multiplication:
(x*y)%z=(x%z*y%z)%z

Example:
(7%3)*(11%3)%3=(1*2)%3=2=(7*11)%3=77%3 (75=3*25)

Hint:

Spoiler:

See the hint for the first question.

Now comes the FUN stuff! Well, if u r stilll with me it must mean u r having fun, right? Right? Well, if u r:
Remember those tricks we used when we were learning the multiplicaction table and what nots? now well prove some of them:

4. Prove that a number is a multiple of 2 if the last digit is a multiple of 2, and that a number is multiple of 5 if the last digit is 0 or 5.

Hint:

Spoiler:

The last digit of a number n can be represented by n%10 (prove it). Decompose a number in r+10*x+100*y+1000*z...; apply the first and the third exercises to reach the conclusion.

5. Prove that a number is multiple of 3 if the sum of its digits is a multiple of 3

Hint:

Spoiler:

Note that 10%3=1; for further hints, see the hint of the previous exercise.

6. What is the last digit of 7^49?

Hint:

Spoiler:

Use the third exercise with 7^i%10, for i=1, 2,.... Do u see a pattern?

So there it is! The idea was to be doable by a lot of ppl (hopefully), and at the same time answering some of the mysteries we might have had on the school. Remember to spoiler ur answers, and leave more puzzles/exercises/challenges!

[Ircher]

1. Prove that % is distributed over addition, that is:
(x+y)%z=(x%z+y%z)%z

Spoiler: My Solution

1. Let x, y, z be arbitrary integers. Let a1 = x % z and a2 = y % z. Then by the definition of module, there exist integers q1 and q2 such that x = q1*z + a1 and y = q2*z + a2. Then, x + y = (q1 * z + a1) + (q2 * z + a2) = (q1 + q2)z + (a1 + a2) = (q1 + q2)z + (x % z + y % z). If 0 <= (x % z + y % z) < z then (x % z + y % z) is clearly the result of (x + y) % z. (Applying % z again to this quantity won't change its value.) If (x % z + y % z) >= z, then we can express (x + y) as (q1 + q2 + 1)z + (x % z + y % z - z). Note that in this case, 0 <= (x % z + y % z - z) < z. (Note that (x % z + y % z < 2z.) Otherwise, x % z + y % z < 0, so (x + y) = (q1 + q2 - 1)z + (x % z + y % z + z), and once more, 0 < (x % z + y % z + z) < z. Thus, (x % z + y % z) % z must be the result of (x + y) % z. Q.E.D.

I will note that #2 is much easier to do by directly applying the definitions of even and odd versus using the module operation.

[word321]

the solution is correct!
and u r right, it is "easy" to prove 2 by hand; but I blv it is more of an issue with notation. The core principle of doing it directly and using the % notation is the same, calling the same thing with different names; but I left it there just to illustrate the logic to be used in further demostrations (so ppl can "adapt" to "adding things module something").

[StrangerCoug]

Let z₁ and z₂ be two complex numbers whose magnitudes are r₁ and r₂ respectively and whose phases are φ₁ and φ₂ respectively. Prove algebraically that z₁z₂ = r₁r₂ cis(φ₁ + φ₂), where cis(φ) = cos(φ) + i sin(φ).

[D3f3nd3r]

I’d love to see if I remember how to do this, but as an electrical engineer I’m pretty sure I’d get forced out of this thread for my use of j.

[StrangerCoug]

I will understand you if you use j. Thanks for the heads up.

[D3f3nd3r]

I mean if anyone else wants it go ahead, I’m only about a year and a half removed from my complex variables class...

[StrangerCoug]

Let z₁ and z₂ be two complex numbers whose magnitudes are r₁ and r₂ respectively and whose phases are φ₁ and φ₂ respectively. Prove algebraically that z₁z₂ = r₁r₂ cis(φ₁ + φ₂), where cis(φ) = cos(φ) + i sin(φ).

Spoiler: Hint

How do you convert between the rectangular form and the polar form of a complex number?

[Ircher]

Let z₁ and z₂ be two complex numbers whose magnitudes are r₁ and r₂ respectively and whose phases are φ₁ and φ₂ respectively. Prove algebraically that z₁z₂ = r₁r₂ cis(φ₁ + φ₂), where cis(φ) = cos(φ) + i sin(φ).

Spoiler: My Attempt

Let z1 and z2 be complex numbers with magnitudes r1 and r2 and phases phi1 and phi2 respectively. Then (in polar form), z1 = r1(cos(phi1) + i * sin(phi1)) and z2 = r2(cos(phi2) + i * sin(phi2)). Then:

z1z2 = (r1*cos(phi1) + i * r1 * sin(phi1)) * (r2 * cos(phi2) + i * r2 * sin(phi2))
= r1 * r2 * cos(phi1) * cos(phi2) + i * r1 * r2 * cos(phi1) * sin(phi2) + i * r1 * r2 * sin(phi1) * cos(phi1) + i * i * r1 * r2 * sin(phi1) * sin(phi2)
= r1 * r2 * (cos(phi1) * cos(phi2) + i * cos(phi1) * sin(phi2) + i * cos(phi2) * sin(phi1) - sin(phi1) * sin(phi2)
= r1 * r2 * (cos(phi1 + phi2) + i * sin(phi1 + phi2))
= r1 * r2 * cis(phi1 + phi2).\box

Not too bad of a problem.

[StrangerCoug]

Spoiler: Response to Ircher's attempt

= r1 * r2 * (cos(phi1) * cos(phi2) + i * cos(phi1) * sin(phi2) + i * cos(phi2) * sin(phi1) - sin(phi1) * sin(phi2)

You have an unmatched parenthesis on this line. Where should the other closing parenthesis go?

[Ircher]

Spoiler: Response to Ircher's attempt

= r1 * r2 * (cos(phi1) * cos(phi2) + i * cos(phi1) * sin(phi2) + i * cos(phi2) * sin(phi1) - sin(phi1) * sin(phi2)

You have an unmatched parenthesis on this line. Where should the other closing parenthesis go?

Spoiler:

Ah, it should go at the end of the line, so revised proof:

Let z1 and z2 be complex numbers with magnitudes r1 and r2 and phases phi1 and phi2 respectively. Then (in polar form), z1 = r1(cos(phi1) + i * sin(phi1)) and z2 = r2(cos(phi2) + i * sin(phi2)). Then:

z1z2 = (r1*cos(phi1) + i * r1 * sin(phi1)) * (r2 * cos(phi2) + i * r2 * sin(phi2))
= r1 * r2 * cos(phi1) * cos(phi2) + i * r1 * r2 * cos(phi1) * sin(phi2) + i * r1 * r2 * sin(phi1) * cos(phi1) + i * i * r1 * r2 * sin(phi1) * sin(phi2)
= r1 * r2 * (cos(phi1) * cos(phi2) + i * cos(phi1) * sin(phi2) + i * cos(phi2) * sin(phi1) - sin(phi1) * sin(phi2))
= r1 * r2 * (cos(phi1 + phi2) + i * sin(phi1 + phi2))
= r1 * r2 * cis(phi1 + phi2).\box

[StrangerCoug]

Spoiler: Response to Ircher's attempt

= r1 * r2 * (cos(phi1) * cos(phi2) + i * cos(phi1) * sin(phi2) + i * cos(phi2) * sin(phi1) - sin(phi1) * sin(phi2)

You have an unmatched parenthesis on this line. Where should the other closing parenthesis go?

Spoiler:

Ah, it should go at the end of the line, so revised proof:

Let z1 and z2 be complex numbers with magnitudes r1 and r2 and phases phi1 and phi2 respectively. Then (in polar form), z1 = r1(cos(phi1) + i * sin(phi1)) and z2 = r2(cos(phi2) + i * sin(phi2)). Then:

z1z2 = (r1*cos(phi1) + i * r1 * sin(phi1)) * (r2 * cos(phi2) + i * r2 * sin(phi2))
= r1 * r2 * cos(phi1) * cos(phi2) + i * r1 * r2 * cos(phi1) * sin(phi2) + i * r1 * r2 * sin(phi1) * cos(phi1) + i * i * r1 * r2 * sin(phi1) * sin(phi2)
= r1 * r2 * (cos(phi1) * cos(phi2) + i * cos(phi1) * sin(phi2) + i * cos(phi2) * sin(phi1) - sin(phi1) * sin(phi2))
= r1 * r2 * (cos(phi1 + phi2) + i * sin(phi1 + phi2))
= r1 * r2 * cis(phi1 + phi2).\box

Spoiler:

Looks good